This can be read along with the initial
semisync post. This post was shared on code.google.com many years ago but code.google has been shutdown. It describes work done by my team at Google. I am interested in the history of technology and with some spare time have been enable to republish it.
Semisync replication was designed and implemented by
Wei Li. He did a lot of work to make replication better for web-scale and then moved away from MySQL. Upstream reimplemented the feature which was a good decision given the constraints on our implementation time.
Introduction
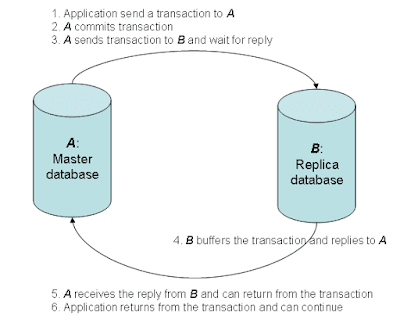
Semi-sync replication blocks return from commit on a master until at least one slave acknowledges receipt of all replication events for that transaction. Note that the transaction is committed on the master first.
Background
MySQL replication is asynchronous. If a master fails after committing a transaction but before a slave copied replication events for that transaction, the transaction might be lost forever. For some deployments, we prefer to reduce the chance of this.
The asynchronous replication model might lose user-visible transactions during a unplanned failover. If the master crashes and we let a slave take over, then the application must be prepared to check which transactions actually made it to the slave, and rerun the ones that did not.
Overview
To solve the asynchronous problem, we can add different degrees of synchronicity: fully synchronous replication would wait for the slave to process the transaction first, before telling the client that it has been committed. The downside: delays in commits.
We propose to do semi-synchronous replication: before telling the client that a transaction has been committed, make sure that the slave receives its replication events first. This is also called 2-safe replication. Below is the picture of a semi-synchronous replication:
MySQL commit protocol
The commit protocol is different between MySQL-4.x and MySQL-5.0. The main reason is because MySQL-5.0 uses two phase commit to make sure binlog status conforms to transactional storage engines' internal status.
- MySQL-4.x
- write the transaction in the binlog file
- commit the transaction in InnoDB or other storage engine
- MySQL-5.0:
- prepare the transaction in InnoDB or other storage engines
- write the transaction in the binlog file - this is considered as the commit point
- commit the transaction in InnoDB or other storage engines
Semi-synchronous commit protocol
Our proposed semi-synchronous replication works in the following way:
- commit the transaction
- wait for the replica databases acknowledge that they already received the transaction - this step has a timeout
- tell the client that the commit has been processed
The committed transaction would not wait indefinitely for the replication thread to send the binlog event. If so, the transaction would never commit if there are network issues or the slave database is down. In step-2, the committed transaction will timeout after a predefined waiting time.
After the timeout, the semi-synchronous replication will be disabled. A new replication thread can catch up in replication and enables it again.
During the wait for network acknowledgment, other transaction would not be blocked and can still continue.
The following global counters will be added:
- transaction failure timeouts
- transactions without going through semi-synchronous replication
- network timeouts
TCP/IP is not enough for acknowledgment
The tricky thing is that replication thread calls TCP/IP to send the replication events. Note that TCP/IP, even with the TCP_NODELAY option does not guarantee that the slave has received the data. Thus, to make sure that the slave database has got the transaction, the slave database must give us an reply to indicate that. This means a transaction commit requires at least a TCP round-trip time. Considering that the round-trip time in one data center is 0.5ms, this should not prevent MySQL from achieving above hundreds of transaction per second.
We will also provide the option of sending the transaction without waiting for the confirmation. We can measure the performance difference to understand the network overhead in the synchronous replication. A parameter will be provided to dynamically change the timeout.
Replication protocol changes
To guarantee that a slave database has got the transaction, the slave database must send one reply message back. This is the situation:
- the master database need to know when to wait for the reply from the slave database; right now, the master database never waits
- the slave database need to know when it should send reply message to the master master database
- we can not do the ping-pong process for every replication event; it can only work for one transaction to minimize the network overhead
In this way, we must have a way for both the master and the slave know when to start this confirmation process. So, any design without replication event changes or replication protocol changes is not possible because the slave database can only figure out the information from the received message. Initially, we wanted to make the replication event change that one special event is appended after a transaction to indicate the slave waiting. However, since replication logs will be served at least once for each replica, this turns out to be a bad idea because we wait only once during transaction commit time.
The only solution after this is to make replication protocol changes. This is the current MySQL replication login process:
- on the slave database side:
- a slave database calls safe_connect() to login to the master database
- COM_BINLOG_DUMP command is sent to the master database to request for binlogs with the following information: binlog_filename, binlog_pos, binlog_flag, server_id
- on the master database side:
- COM_BINLOG_DUMP is handled to recognize the requested dump information
- mysql_binlog_send() is called to send the requested binlog events
Because binlog_flag is sent from the slave database and processed in the master database, semi-synchronous replication will be initiated by the slave and the replication thread will trigger the synchronous operation in the master database. We add one bit in binlog_flag so that the slave database can register itself as synchronous replication target.
* #define BINLOG_SEMI_SYNC 0x02
If BINLOG_SEMI_SYNC is set for the replication thread, then every event sent from the master database to the slave database will always have one byte extra header. The one byte indicates whether the replication thread is expecting the reply from the slave database. In this way, the new replication protocol's usage is session-based.
Work on the master database side
We will create a search tree that records all waiting transactions. The tree will be keyed on (binlog_filename, binlog_pos). At transaction commit time, after all transaction events have been written into the binlog file, we insert the (binlog_filename, binlog_pos) into the search tree. The purpose of the search tree is for the replication thread to recognize the current waiting transactions. When a transaction stops waiting for the reacknowledgment of the binlog events, the transaction's position should be removed from the tree.
The replication thread reads a binlog event from the file and probe the binlog position into the search tree. Depending on whether the position in the search tree, the replication thread will set the one byte extra header before sending the event.
Work on the slave database side
If a slave database is connecting with the semi-synchronous replication mode, it will check the first byte header to decide whether to reply the replication event. Otherwise, it work as original.
Currently, the master database uses one mutex LOCK_log to synchronize all operations on the binlog:
- a transaction acquires LOCK_log before writing transaction events to a binlog
- the transaction releases LOCK_log after committing and flushing the binlog to the file system
- replication thread acquires LOCK_log before reading each event and release the lock afterwards
In semi-synchronous replication, we are planning to add one mutex and one condition variable:
- innobase_repl_semi_cond: this variable is signaled when enough binlog has been sent to slave, so that a waiting transaction can return the 'ok' message to the client for a commit
- innobase_repl_semi_cond_mutex: the mutex that is associated with the above condition variable
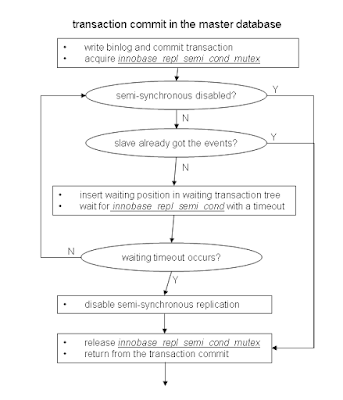
Code flow for each MySQL session during transaction commit
- write all binlog events, append the transaction-end event and flush the file to the filesystem
- commit the transaction inside InnoDB
- acquire innobase_repl_semi_cond_mutex
- while true:
- if semi-synchronous replication has been disabled by timeout:
- update the asynchronous transaction counter
- release innobase_repl_semi_cond_mutex and return from the commit
- check the current binlog sending status
- if the binlog sending status is ahead of my transaction's waiting position
- release innobase_repl_semi_cond_mutex and return from the commit
- set my binlog waiting position to my commited transaction position
- wait for innobase_repl_semi_cond with a timeout
- if timeout occurs with waiting innobase_repl_semi_cond or if semi-synchronous replication is disabled after wake-up
- print the error message
- update failed timeout counter
- disable the semi-synchronous replication until the replication thread enables it again
- release innobase_repl_semi_cond_mutex and return from the commit
Code flow for replication thread
This is the work done by the replication thread when sending binlog events to support the semi-synchronous protocol.
- if the replication is not the semi-synchronous target, then do nothing and simply return
- if the most recent sent event is NOT an transaction-end event, then do nothing and simply return
- wait for the confirmation from the slave database with a network timeout
- remember whether network timeout occurs
- acquire innobase_repl_semi_cond_mutex
- if the network timeout occurs:
- update failed timeout counter
- disable the semi-synchronous replication until the replication thread enables it again
- release innobase_repl_semi_cond_mutex and return
- if the semi-synchronous replication is disabled, then enable the semi-synchronous replication again
- check whether any session is waiting for the current sending position
- if there exist such sessions, wake them up through innobase_repl_semi_cond
- release innobase_repl_semi_cond_mutex and return

The only one mutex/condition variable create one synchronize point because every committed transaction needs to wait for innobase_repl_semi_cond. When the replication thread wakes up innobase_repl_semi_cond, it has to use broadcast. This might be changed in the future if there are performance issues around the single mutex wait.
Codeflow for replication I/O thread connection to the primary database
When a replica connects to the primary database, it is an opportunity for the primary database to understand the replica's progress. Based on the progress, the primary database will adjust semi-synchronous replication's progress. If the replica's status is too behind, semi-synchronous replication might be suspened until the replica is fully caught up.
If there is only one semi-synchronous target, meaning just one thread is sending the binlog to the slave for which we want synchronous replication, then the replication position should increase monotonically. However, we want to have more than one semi-synchronous replica target to increase the primary database's transaction availability. In that sense, a falling behind replica should not affect the status on the primary if others are caught up.
Network group commit
Replication threads can do group commit to minimize network overhead. When the thread finds the current sending event is a end of transaction event, it would request for a reply from the slave database immediately. Instead, it look for the tail of the binlog file to check whether there are more transaction. Or, it can wait for a while to make the check. If there are more transactions in the file, the replication thread can send all waiting transactions and only waits for one reply. This looks like that we are doing group commit on the network.
The benefit is that we can reduce network round trip by batching transaction replies. However, it also reduces the reliability of semi-synchronous replication. If we acknowledge each transaction, we can only lose at most one transaction during failure. If we do group commit, we might lose all transactions in the batch. We need to trade off between performance and reliability.