I often see benchmark results for an LSM tree where the shape of the tree is not described. When the results are worse than desired I wonder how much of that is inherent to the LSM tree versus the configuration. It might be easier to make an LSM tree look bad than to make a B-Tree look bad.
I have results from RocksDB for which QPS varies by up to 5X depending on the shape of the LSM tree. The workload is read-only and CPU-bound. The impact of the LSM tree shape on CPU overhead is known but not widely known. Hopefully this helps with that.
Read amplification for an LSM is usually worse than for a B-Tree. But read-amp should be described separately for IO vs CPU because (usually) CPU read-amp is the problem. The unit for IO read-amp is pages read from storage (real storage, not a read from the OS page cache). The unit for CPU read-amp is CPU overhead but some combination of cache lines read, keys compared and bloom filters checked per query might be a good proxy.
The extra CPU read-amp comes from the number of trees in the LSM tree that must be searched on queries. Perhaps LSM tree is a misnomer because it usually has more than one tree, but perhaps not enough trees for LSM forest to be a good name. Is it too late to rename LSM tree to LSM trees? The memtable is one tree, each sorted run in the L0 is another tree, and then each level beyond L0 is one more tree. For the configurations I use it is common for there to be from 10 to 20 trees in one RocksDB instance. While bloom filters help, they don't eliminate the overhead. Even with a bloom filter some searching is done (cost is a function of |values|) and then there is the overhead of the bloom filter check. For too much information on the CPU overhead of a RocksDB query, see this post from me.
I will begin using LSM tree shape to describe the state of the LSM tree where the state includes:
- number of KV pairs in the active memtable
- number of immutable memtables waiting to be flushed
- number of sorted runs in the L0
- number of levels beyond the L0, and their sizes
- Flushing the memtable has no impact on throughput
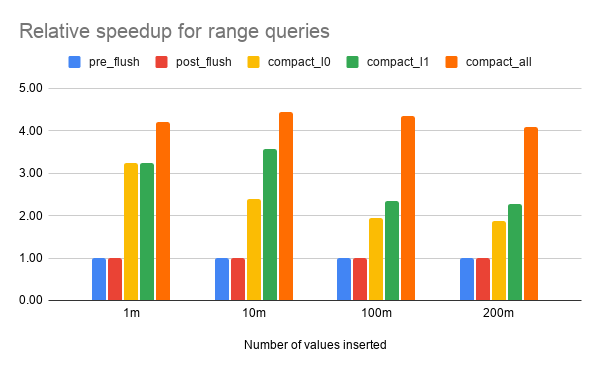
- The impact from too many trees to search is worse for workloads that don't use bloom filters (like range queries, or any queries when bloom filters don't exist). The worst-case was ~5X for range and point without bloom vs ~2X for point with bloom.
- There are incremental benefits from compacting the L0, compacting the L1 and doing full compaction. Each of these reduces the number of trees to search.
- Bloom filters in an LSM aren't O(1). There is a search cost, O(logN), to find per-SST filter
- Feature request for LSM trees - adapt to be more read-friendly when a workload is read-heavy
- This is more of an issue for read-only benchmarks because the LSM tree shape is usually stuck in the same state for the duration of the test. That state might be good or bad and this can add noise or misleading results to your tests. For a test with writes the LSM tree is likely to have data in all places (memtable, L0, L1, ...) most of the time which might not help read performance but will reduce read response time variance.
My tests
I ran tests for three types of queries: short range queries, point queries with bloom filters and point queries without bloom filters. I repeated the queries for four LSM tree shapes described below. By data is in the memtable I mean that the memtable is at least half full but there were no immutable memtables. By data is in L0 I mean there were six SSTs (sorted runs) in L0.
- pre_flush - data is in the memtable, L0 and each level beyond L0
- post_flush - memtable is empty while L0 and larger levels have data
- compact_l0 - memtable and L0 are empty while L1 and larger levels have data
- compact_l1 - memtable, L0 and L1 are empty while L2 and larger levels have data
- compact_all - all data is in one sorted run on Lmax (the max level of the LSM tree)
- flush - flushes the memtable
- compact0 - compacts L0 into L1 (and blocks until done)
- compact1 - compacts L1 into L2 (and blocks until done)
- waitforcompaction - a hacky attempt to block until compaction is done. Can be used as --benchmarks=fillrandom,compactall,waitforcompaction,readrandom because compactall doesn't block until compaction is done.
db_bench ... --benchmarks=fillrandom,flush,waitforcompaction,compact0
db_bench ... --use_existing_db=1 --benchmarks=overwrite,waitforcompaction,...
For all tests the target size for L1 is 64M and dynamic leveled compaction was enabled. But the interaction between dynamic leveled and my configuration means that the LSM trees for the 10M and 100M values tests use the same number of levels with a dramatically different sizeof(L1) / sizeof(L0) ratio. That ratio is <= 2 for the 10M values test vs ~10 for the 100M values test. The LSM tree uses one too many levels in the 10M values test.
LSM tree shape by number of values inserted when per-level fanout is 10 (default):
- 1M
- memtable is ~80% full with 38,239 values
- L0 has 6 sorted runs and 33M of data
- L1 has 87M of data
- 10M
- memtable is ~80% full with 38,199 values
- L0 has 6 sorted run and 34M of data
- L1 has 80M of data
- L2 has 829M of data
- 100M
- memtable is ~80% full with 38,240 values
- L0 has 6 sorted runs and 39M of data
- L1 has 792M of data
- L2 has 7.77G of data
- 200M
- memtable is ~80% full with 38,215 values
- L0 has 6 sorted runs and 38M of data
- L1 has 163M of data
- L2 has 1.61G of data
- L3 has 16.12G of data
- 1M
- memtable is ~80% full with 38,209 values
- L0 has 6 sorted runs and 33M of data
- L1 has 87M of data
- 10M
- memtable is ~80% full with 38,241 values
- L0 has 6 sorted runs and 34M of data
- L1 has 101M of data
- L2 has 820M of data
- 100M
- memtable is ~80% full with 38,264 values
- L0 has 6 sorted runs and 39M of data
- L1 has 126M of data
- L2 has 1.0G of data
- L3 has 7.9G of data
- 200M
- memtable is ~80% full with 38,215 values
- L0 has 6 sorted runs with 38M of data
- L1 has 251M of data
- L2 has 1.98G of data
- L3 has 15.83G of data


No comments:
Post a Comment